Roule Ta Bille

mars 2017 physique, modélisation

Roule ta bille

L'idée est de faire un circuit de bille périodique, sans mécanisme pour remonter la bille autre que la force centrifuge, donnée par la rotation de l'ensemble du circuit. L'énergie vient de la rotation constante de la structure, imposée par un moteur.

Il n'y a pas de balais, ou de pièce non tournante, qui vient bloquer la bille dans son mouvement, pour la pousser le long d'une rampe.

Montée

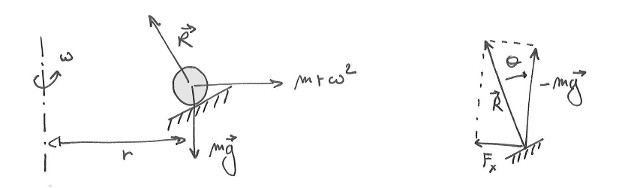
schema 1

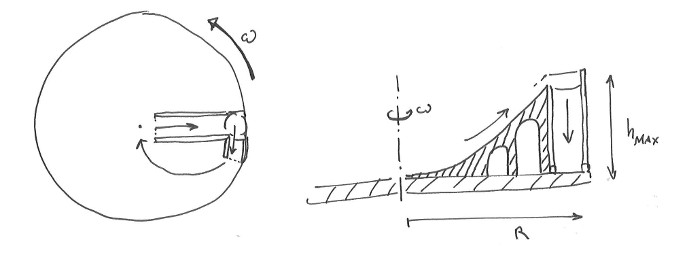
Pour la montée la bille est dans une gorge radiale. Les forces en présence sont donc la gravité, la réaction du support et la force centrifuge (en se plaçant dans le référentiel tournant). L'accélération est négligée pour le moment. Si $\theta$ est l'angle du support avec l'horizontal, $g$ l'accélération de la gravité, $\omega$ la vitesse de rotation (rad/s), $r$ le rayon où se trouve la bille, la somme des forces projetée sur l'horizontale donne: (la masse se simplifie)

$g.\tan(\theta) = r.\omega^2$

donc la pente permettant l'équilibre des forces sur la bille est pour chaque position $r$ :

$\theta\left(r\right) = \arctan\left( \frac{\omega^2}{g} r \right)$

Si on se limite à un système de rayon $R$, la hauteur maximale atteignable, pour une certaine vitesse de rotation $\omega$ est (merci Wolfram):

$$ h_{max} = \int_0^R \theta(r)dr = R\,\arctan\left( \frac{\omega^2}{g} R\right) - \frac{g}{2\omega^2} \ln\left[ 1 + \left(\frac{\omega^2}{g} R\right)^2 \right] $$
In [63]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
In [64]:
g = 9.81 # m.s-2
h_max = lambda  R, w: R*np.arctan( w**2/g*R ) - g/2.0/w**2*np.log( 1 + (w**2/g*R)**2 )
In [128]:
Rmax = 8e-2
w = 2*np.pi*45.0/60.0

r_span = np.linspace(0, Rmax, 55)
profil = np.vectorize( h_max )

plt.figure(figsize=(11, 3))
plt.plot( r_span*100, profil(r_span, w)*100  ), plt.plot( r_span*100, r_span*0, ':'  )
plt.xlabel('r (cm)'); plt.ylabel('h_max (cm)'); plt.title('w=%0.2f rad/s'%w); plt.axis('equal')
Out[128]:
(0.0, 8.0, 0.0, 0.80000000000000004)
In [66]:
w_span = np.pi*2*np.logspace(-1, 3, 45)
h_max_w = np.vectorize( h_max, excluded=['R'] )

R = 10e-2
plt.semilogx( w_span/np.pi/2, h_max_w(R, w_span)*100  )
plt.xlabel('w/2pi (Hz)'); plt.ylabel('h_max (cm)'); plt.title('R=%0.2f m' % R)
Out[66]:
<matplotlib.text.Text at 0x7f3d81c94790>

Remarque: il est plus interessant d'avoir $w>1-2\,Hz$, mais voir la suite...

Si on compare l'énergie potentiel acquise ($g\,h_{max}$) avec l'énergie cinétique acquise aussi ($(\omega\,R)^2/2$):

In [67]:
R = 100e-2
w = 2*np.pi*2

print 'E potentiel:', g*h_max(R, w)
print 'E cinétique:', (w*R)**2/2.0

E potentiel: 13.1063294594
E cinétique: 78.9568352087

Descente (c.a.d. retour au centre)

schema 2

Notation pour la trajectoire circulaire de retour, dans le reférentiel fixe (x, y): 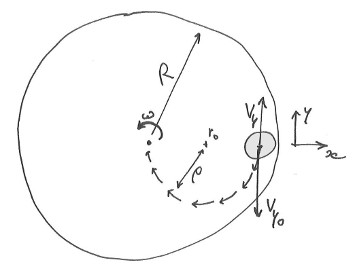schema 2

Un bille sur un plateau tournant plat et lisse a des trajectoires stable circulaire (cf publi & video). C.a.d. sans frottement et force extérieure.

  • La vitesse de rotation sur cette trajectoire est donnée par $w_c = 2/7 w$, pour une bille pleine (cf. moment d'inertie d'une sphère).
  • Le rayon de la trajectoire circulaire est $\rho = |v_0|/w_c$, avec $v_0 = [v_{0x},\, v_{0y}]$ le vecteur vitesse initiale (dans le ref. du labo)
  • Le centre du cercle est en $r_c = [ x_0 - v_{0y}/w_c,\, y_0 + v_{0x}/w_c ]$, toujours dans le ref. du labo, avec $[x_0,\, y_0]$ la position initial de la bille. On fixe: $x_0 = R$ et $y_0=0$
  • La condition pour que la trajectoire de la bille passe par le centre est: $\rho = |r_c|$

Cette dernière relation permet d'aboutir à: $$ v_{0y} = \frac{R\,w_c}{2} $$

La bille passera alors par le centre quelque soit la composante $v_{0x}$. Cette vitesse est dans le réferentiel du labo.

  • La vitesse tangentiel de la bille, à la fin de la rampe de montée, sera: $v_y = w\,R$
  • La variation de vitesse $\Delta v$ nécessaire pour injecter la bille sur la bonne trajectoire est donc: $$ \Delta v = v_{0y} - v_y = \frac{R\,w_c}{2} - w\,R $$

qui se simplifie: $$ \Delta v = -\frac{6}{7}w\,R $$

Cela signifie que la bille doit perdre environ 85% de sa vitesse (tangentielle) dans ref. du labo.

L'énergie pour effectuer ce changement de vitesse va être donnée par l'énergie potentielle obtenue lors de la montée: $E_p = m\,g\,h_{max}$. L'énergie cinétique est $m\,v^2/2$. Donc la variation de vitesse maximale est:

$$ \Delta v_{max} = \sqrt{ 2\,g\,h_{max} } $$

La condition pour que la bille puisse revenir au centre est : $\Delta v_{max} > \Delta v$

In [68]:
R = 10e-2
w = 2*np.pi*1
In [69]:
print np.sqrt( 2*g*h_max(R, w))
print 6.0/7.0*w*R

0.620293575553
0.538558740615
In [70]:
dv_max = lambda w: np.sqrt( 2*g*h_max(R, w))
dv = lambda w: 6.0/7.0*w*R
In [77]:
w_span = np.pi*2*np.logspace(-1, 1, 75)
h_max_w = np.vectorize( h_max, excluded=['R'] )

R = 5e-2 # m

f, (ax1, ax2, ax3) = plt.subplots( 3, sharex=True, figsize=(9,9))

ax1.semilogx( w_span/np.pi/2, dv_max(w_span), label='\Delta v max'  )
ax1.semilogx( w_span/np.pi/2, dv(w_span) , label='\Delta v'  )

ax1.set_ylim([.0, 1.5])
ax1.set_title('(Delta v max - Delta v)')
#ax.xlabel('w/2pi (Hz)'); ax.ylabel('dv (m/S)'); ax.title('R=%0.2f m' % R)
ax1 = ax1.legend(loc='upper left')

ax2.semilogx( w_span/np.pi/2, (dv_max(w_span)-dv(w_span)), label='Delta v max - Delta v '  )

#ax.xlabel('w/2pi (Hz)'); ax.ylabel('dv (m/S)'); ax.title('R=%0.2f m' % R)
#ax = ax.legend(loc='upper center')
ax2.set_ylim([.0, .08])
ax2.set_ylabel('delta delta (m/s)'); 

taux = (dv_max(w_span)-dv(w_span))/dv(w_span)*100
ax3.semilogx( w_span/np.pi/2, taux, label='Delta v max - Delta v '  )

#ax.xlabel('w/2pi (Hz)'); ax.ylabel('dv (m/S)'); ax.title('R=%0.2f m' % R)
#ax = ax.legend(loc='upper center')
ax3.set_ylim([.0, 20])
ax3.set_ylabel('%'); ax3.set_xlabel('w/2pi (Hz)'); 

f.subplots_adjust(hspace=.03)

Il y a donc une vitesse de rotation maximale au-dèla de laquelle il n'est plus possible pour la bille de revenir au centre (avec ce type de trajectoire)... l'énergie cinétique augmente indefiniment, alors que l'énergie potentielle sature quand $w$ augmente pour un rayon max. $R$ constant...

In [81]:
dv_max = lambda w: np.sqrt( 2*g*h_max(R, w))

dh = lambda R, w: (6.0/7.0*R*w)**2/2.0/g
In [143]:
Rmax = 8e-2
w = 2*np.pi*45.0/60.0

hmax = h_max( Rmax, w )
print( hmax*1000 )

print dh( Rmax, w )*1000

7.2046637809
5.32193609345

Quelle est la trajectoire de la bille dans le ref. tournant ?

In [116]:
def Utournant( t, rho, w_c ):
    theta = w_c*t
    ux = rho*( 1 + np.cos(theta) ) 
    uy = rho*np.sin( theta )
    
    r = np.sqrt( ux**2 + uy**2 )
    phi = np.arctan2( uy, ux )
 
    
    Ur, Uphi = U_fixe( t, rho, w_c )

    Ur_prime = Ur
    Uphi_prime = Uphi - w*t

    Ux = Ur_prime*np.cos( Uphi_prime )
    Uy = Ur_prime*np.sin( Uphi_prime )
    
    return Ux, Uy
In [137]:
R = 8e-2
w = 2*np.pi*45.0/60.0

rho = R/2.0
w_c = 2.0/7.0*w

time = np.linspace( 0, np.pi/w_c, 51 )

Ux, Uy = Utournant(time, rho, w_c)
In [138]:
ax=plt.subplot(aspect='equal')
ax.add_artist( plt.Circle((0, 0), 100*R, alpha=0.05) )

ax.plot( Ux*100, Uy*100, 'x-' )
Out[138]:
[<matplotlib.lines.Line2D at 0x7f3d7bd6f7d0>]
In [139]:
plt.plot( time, Uy )
Out[139]:
[<matplotlib.lines.Line2D at 0x7f3d7bca44d0>]
In [140]:
whereItIs( 1 )
Out[140]:
0.0023912918943382699
In [141]:
from scipy.optimize import minimize

whereItIs = lambda t:  Utournant(t, rho, w_c)[1]**2
sol = minimize(whereItIs, 1.6)

tZero = sol.x[0]

print 100*np.array( Utournant(tZero, rho, w_c) )

rZero = Utournant(tZero, rho, w_c)[0]
h_max( rZero, w  )*1000

[  3.99949801e+00  -1.73738038e-03]
Out[141]:
1.8080168334031619

Questions bonus:

  • Est-ce qu'il est possible de faire plusieurs rampe succesif our gagner en hauteur ? descendre de 1/2 $h_max$ et remonter plus haut ?
  • Version cylindre vertical avec la bille à l'intérieure ...
In [76]: